http://rsc.hyperlinx.cz/casio/kalkulacky/programy.php
[ Archaikum.cz > CASIO > grafické kalkulačky > Programy do kalkulačky ]
Sponzorované odkazy:

Programy do kalkulačkyT



 Matematika   Geodézie   Kartografie   Astronomie   Teorie chyb   Optika   Různé 

Matematika

Dělení polynomu polynomem (498 B) (194 B)
Do matice A zadej dělenec (čitatel), do matice B dělitel (jmenovatel) - obě matice jsou sloupcové - a spusť program. Zobrazí se ti celá část a čitatel případného zbytku (jmenovatel je shodný s původním). Výsledky se uloží do matic C (celá část) a D (čitatel zbytku)

Numerické řešení diferenciálních rovnic (818 B)
Runge-Kuttova metoda (414 B)
zadáš pravou stranu diferenciální rovnice y' = , bod, interval a krok po němž se v intervalu postupuje
Zápis do Listů:
List 1: body na ose X
List 2: hodnoty Runge-Kuttovy metody prvního řádu
List 3: hodnoty Runge-Kuttovy metody druhého řádu

Numerický výpočet určitého integrálu (1.44 kB)
Lichoběžníková metoda (322 B)
zadáš funkci y = , interval a krok po němž se v intervalu postupuje. Výsledkem je číselná hodnota (plocha pod grafem) integrálu a přesnost výpočtu
Zápis do Listů:
List 1: body na ose X
List 2: funkční hodnoty na ose Y
List 3: absolutní hodnota maxima funkce v daném bodě

Simpsonova metoda (432 B)
zadáš funkci y = , interval a krok po němž se v intervalu postupuje (počet kroků musí být sudý). Výsledkem je číselná hodnota (plocha pod grafem) integrálu a přesnost výpočtu (do paměti fn2 je nutné zadat čtvrtou derivaci funkce kterou počítáš)
Zápis do Listů:
List 1: body na ose X
List 2: funkční hodnoty na ose Y
List 3: absolutní hodnota maxima funkce v daném bodě

Matice (1.02 kB) - Gaussova eliminace matice (pracuje se s maticí Z)
Matice_1 (168 B) - vytvoří horní trojuhelníkovou (lichoběžníkovou) matici
Matice_2 (215 B) - vytvoří dolní trojuhelníkovou (lichoběžníkovou) matici

HERON+ (664 B) (330 B) - po zadání délky stran trojuhelníku vypočte jeho obvod, obsah a velikost vnitřních úhlů

Geodézie

Směrník a délka (0.81 KB): YX-rθ (244 B)
Průsečík přímek (0.94 KB): PRUSECIK (344 B)
Průsečík přímky a kružnice (0.97 KB): PRUS_p_k (600 B)
Tachymetrický zápisník (754 B): TACHYMET (237 B)

Centrace a redukce zenitky na excentrickém stanovisku pro nenulovou výšku cíle (2.23 kB)  
ZENIT (532 B) - výpočet pomocí postupných aproximací (čtyři iterační kroky)
ZENIT2 (535 B) - to samé co předchozí program, ale s výpisem mezivýsledků

MGÚ - chybové modely základních geodetických úloh (7.75 kB) - určení chybového modelu základních geodetických úloh
- Souřadnice bodů se zadávají v metrech, chyba délky a střední souřadnicová chyba daných bodů v milimetrech a chyba směrů ve vteřinách (grádových nebo šedesátinných, podle aktivní úhlové míry)
- Pokud neznáš střední souřadnicovou chybu daných bodů mxy, zadej hodnotu 0 a výpočet se provede bez vlivu základu. Pokud místo celkové chyby mxy znáš jednotlivé chyby mx a my, je třeba zadat jejich čtverce (hodnota na druhou) na diagonálu Matice X a to v pořadí mx bodu A, my bodu A, mx bodu B, my bodu B, ... a poté spustit program MGU. Předtím je ale třeba zadat ostatní hodnoty přes příslušný program MGU_xxx
- Obdobně je možné při různých přesnostech jednotlivých měřených směrů v matici T zadat čtverce jednotlivých chyb směrů a délek. Pořadí jejich zápisu je uvedeno níže v závorce za názvem programu
MGU (863 B) - podprogram sloužící k vlastním výpočtu MGÚ - následující programy slouží k zadání vstupních souřadnic a chyb měřených směrů, délek a daných bodů a tento program vypočte kovarianční matice, střední chyby (mx, my, mp a mxy) a parametry elipsy chyb (úhel stočení ω a délky poloos a a b)
MGU_HANS (797 B) - Hansenova úloha (ψPA, ψPB, ψPQ, ψQP, ψQA, ψQB)
MGU_P_DE (367 B) - protínání vpřed z délek (sAP, sBP)
MGU_P_UH (567 B) - protínání vpřed z úhlů (ψAP, ψAB, ψBA, ψBP)
MGU_P_Z (578 B) - protínání zpět (ψPA, ψPB, ψPC)
MGU_RAJ (521 B) - rajón (ψAB, ψAP, sAP)
MGU_RAJZ (524 B) - zpětný rajón (ψPA, ψPB, sPA)
MGU_rθ (530 B) - změna délky r a směrníku θ na základě změny polohy koncových bodů úsečky. Vypočte změnu a střední chybu směrníku a délky

Zápis do Matic
Matice A: Jacobiho matice vztahu mezi konfiguračními a zprostředkujícími parametry odpovídající určovaným bodům (matice A1)
Matice B: inverzní matice k matici A
Matice C: Jacobiho matice vztahu mezi konfiguračními a zprostředkujícími parametry odpovídající daným bodům (matice A2)
Matice D: Jacobiho matice vztahu mezi měřenými a zprostředkujícími parametry
Matice M: kovarianční matice vlivu měření (matice Mm)
Matice N: kovarianční matice vlivu základu (daných bodů) (matice Mx)
Matice O: celková kovarianční matice vlivu měření a základu (matice Mp)
Matice T: diagonální matice vyjadřující chyby měřených hodnot
Matice X: diagonální matice vyjadřující chyby daných bodů

Vyrovnání osnovy vodorovných směrů (712 B) 9x50
OSNOVA (321 B) - do Listu 1 až 3 zadej redukované směry změřené osnovy vodorovných směrů (včetně redukovaného směru na počátek (první řádek tedy tvoří nuly)) a spusť program
Spočte se aposteriorní střední chyba měřeného směru m0, střední chyba redukovaného směru mψ a kvadratický průměr řádkových chyb
Zápis do Listů:
List 1: redukované směry v první skupině
List 2: redukované směry v druhé skupině
List 3: redukované směry v třetí skupině
List 4: průměr redukovaných směrů
List 5: střední chyba řádkového průměru

Nepřímé určení centračních prvků z měření tzv. 'malých zenitových úhlů' (1.93 kB) 9x50
EXC-NEP (914 B) - podrobný popis je ve skriptech Geodézie 30 - Výškopis na str. 65 až 66
Zápis do Listů:
List 1: zenitky na jednotlivá rozhraní válcového signálu a na dva znaky na výtyčce v pořadí odshora dolů (poslední je hodnota výsledné zenitky na centr)
List 2: vzdálenosti jednotlivých rozhraní válce od rozhraní nejnižšího oddělené nulou (vzdálenost nejnižšího rozhraní od sebe sama) od výšky znaků na výtyčce
List 3: délka excentricity na jednotlivá rozhraní, průměrná délka excentricity e a její střední chyba me
List 4: opravy e-ei jednotlivých rozhraní válce (vyjde-li me větší než 3mm je vhodné zjistit jestli některá z těchto oprav výrazně nepřevyšuje ostatní, což by mohlo signalizovat možnou chybu odpovídající zenitky)
List 5: výšky rozhraní Xi nad horizontem stroje a jejich střední chyba mX
List 6: oprava 1δ a 2δ zenitek na znaky na výtyčce a příslušné opravené zenitky
List 7: výšky jednotlivých rozhraní válce nad centrem

Redukce šikmé délky (4.61 kB) - matematická redukce šikmé délky do nulové hladiny. Pro převod délky do zobrazovací roviny je třeba výslednou délku vynásobit hodnotou Křovákova koeficientu m (je možné ho určit pomocí programu KROVAK)
REDUKCE (236 B) - po zadání šikmé délky, zenitového úhlu a nadmořské výšky horizontu stroje spočte redukci délky na vodorovnou a do nulové hladiny
REDUKCE1 (139 B) - požadovány přesné nadmořské výšky koncových bodů (odvození je ve skriptech Geodézie - Měření na str. 134)
REDUKCE2 (233 B) - pro převod jsou třeba přibližné výšky koncových bodů a oboustranné zenitky
REDUKCE3 (400 B) - znám výšky koncových bodů, výšku stroje a cíle a oboustranné zenitky. Výpočet probíhá přes spojnici stabilizačních značek (KK) (odvození je ve skriptech Geodézie 30 - Výškopis na str. 62 až 63)
REDUKCE4 (342 B) - to samé co REDUKCE3, ale znám pouze zenitku na stanovisku
REDUKCE5 (279 B) - převod měřené šikmé délky na spojnici stabilizačních značek (KK) při centrickém postavení stroje
REDUKCE6 (512 B) - převod měřené šikmé délky na spojnici stabilizačních značek (KK) při excentrickém postavení stroje
REDUKCE-I (150 B) - inverzní postup matematické redukce - délku v nulové hladině přepočte na spojnici stabilizačních značek (jsou třeba nadmořské výšky koncových bodů)

Určení Křovákova koeficientu (1.00 kB)
KROVAK (184 B) - výpočtu Křovákova koeficientu m pro bodu o známých souřadnicích v S-JTSK)
KROVAK2 (292 B) - výpočtu Křovákova koeficientu m pro přímku (spojnici dvou bodů o známých souřadnicích v S-JTSK)
 

Centrační změny směrů (1.28 kB)  
EXCENT-C (273 B) - centrační změny při excentrickém cíli
EXCENT-S (234 B) - centrační změny při excentrickém stanovisku

Výpočet bodu na kolmici (2.40 kB)
KOLMICE (743 B) - výpočet z údajů zadaných po spuštění programu
KOLMICE2 (422 B) - výpočet z údajů v Listu 3 a 4. Na prvních dvou řádcích jsou známé body včetně souřadnic
Zápis do Listů:
List 1: Y
List 2: X
List 3: staničení
List 4: kolmice
List 5: transformační prvky: λ1, λ2 (transformační koeficienty), M (zkreslení), φ (úhel otočení)
           SAB, SAB´(vzdálenost AB), OP (polohová odchylka), ΔP (mezní odchylka)

Kontrolní oměrné (1.21 k B)
OMERNE (414 B) - výpočet z údajů zadaných po spuštění programu
OMERNE2 (169 B) - výpočet z údajů v Listu 1, 2 a 4 (první oměrná je 0 - dává se vzdálenost na předchozí bod a ten v tomto případě není)
Zápis do Listů:
List 1: Y
List 2: X
List 3: vzdálenost vypočtená ze souřadnic
List 4: oměrná míra
List 5: rozdíl
List 6: mezní rozdíl

Podobnostní transformace (2.06 kB) - podle dvou identických bodů
TRANSFO1 (646 B) - výpočet z údajů zadaných po spuštění programu
TRANSFO2 (416 B) - výpočet z údajů uložených v Listech (na řádku 1 a 2 jsou identické body)
- vypočtené body se ukládají do Listu 1 a 2 pod body identické
Zápis do Listů:
List 1: Y (hlavní soustava)
List 2: X
List 3: Y´ (vedlejší soustava)
List 4: X´
List 5: transformační prvky: λ1, λ2 (transformační koeficienty), M (zkreslení), φ (úhel otočení)
           SPK, SPK´(vzdálenost PK), OP (polohová odchylka), ΔP (mezní odchylka)

Kolineární transformace (1.26 kB)
TRN_Kol (792 B) - výpočet kolineární transformace pomocí 4 identických bodů
- zadej do Listů 1 až 4 souřadnice identických (první čtyři řádky) a podrobných (ostatní řádky) bodů a spusť program. Výsledné souřadnice se uloží do Listu 5 a 6
- začátek zdrojového kódu programu obsahuje obecné transformační rovnice
Zápis do Listů:
List 1: X - identické body v cílové soustavě
List 2: Y
List 3: x - identické body v původní soustavě + body které se budou transformovat
List 4: y
List 5: xT - přetransformované body
List 6: yT

Zápis do Matic:
Matice T: vektor transformačních koeficientů
 

Afinní transformace (996 B)
TRN_Afin (588 B) - výpočet afinní transformace pomocí 3 identických bodů
- zadej do Listů 1 až 4 souřadnice identických (první tři řádky) a podrobných (ostatní řádky) bodů a spusť program. Výsledné souřadnice se uloží do Listu 5 a 6
- začátek zdrojového kódu programu obsahuje obecné transformační rovnice
Zápis do Listů:
List 1: X - identické body v cílové soustavě
List 2: Y
List 3: x - identické body v původní soustavě + body které se budou transformovat
List 4: y
List 5: xT - přetransformované body
List 6: yT

Zápis do Matic:
Matice T: vektor transformačních koeficientů
 

Helmertova transformace v rovině (4.73 kB) 9x50
HELMERT2 (1627 B) - podobnostní transformace řešená pomocí metody nejmenších čtverců pro nadbytečný počet identických bodů
Pokud na řádku 5 změníš '1→Q na 1→Q, vypočte se jako transformace shodnostní
- zadej identické body v hlavní soustavě (List 1 a 2) a ve vedlejší soustavě (List 3 a 4) - každému bodu odpovídá jeden řádek - pod které dej transformované body (stále List 3 a 4) a spusť program HELMERT2
- na displeji se budou zobrazovat informace o jednotlivých krocích transformace
- na konci výpočtu se zobrazí číslo řádku s bodem s maximálním δvv (je podezřelý z neidentity), střední rozdíly souřadnic mY a mX [mm], míra ztotožnění mv [mm2], odhad střední chyby jednotkové m'0 [mm], délkový modul, zkreslení v mm na 100 m a úhel otočení ω. Výsledné souřadnice jsou v Listu 5 a 6
- k programu jsou přidány souřadnice bodů v hlavní a vedlejší soustavě z řešeného příkladu ve skriptech Geodézie 40 - Příklady a návody na cvičení (příklad je na str. 19 až 22)
Zápis do Listů:
List 1: Y - identické body v hlavní soustavě
List 2: X
List 3: Y´ - identické body ve vedlejší soustavě + podrobné body které se budou transformovat
List 4: X´
List 5: YT - výsledné souřadnice transformovaných bodů
List 6: XT
List 7: vy - rozdíl původních a transformovaných souřadnic (YT-Y) a jejich součet Σvy(měl by být 0) v m
List 8: vx
List 9: v - posuny jednotlivých identických bodů v mm
List 10: δvv - poklesy jednotlivých identických bodů v mm2
List 11: označení bodu s maximální hodnotou δvv
List 12: m1yi a m1xi každého bodu v mm (jsou stejné)
List 13: mdi - polohová chyba každého bodu v mm
List 14: poloměr kružnice chyb každého bodu

Zápis do Matic:
Matice A: maticový zápis identických bodů
Matice B: matice (ATA)-1
Matice H: vektor h obsahující souřadnice počátku vlastní soustavy v soustavě hlavní a transformační koeficienty (tx, ty, λ1 a λ2)

Helmertova transformace v prostoru (8.48 kB) 9x50
HELMERT3 (2754 B) - obecná Helmertova transformace v prostoru
HELMERT4 (403 B) - obecná Helmertova transformace v prostoru při známých transformačních koeficientech (neprovádí zápis do Listů)
HELMERT5 (1977 B) - diferenciální Helmertova transformace transformace v prostoru

- zadej identické body v hlavní soustavě (List 1, 2 a 3) a ve vedlejší soustavě (List 4, 5 a 6) - každému bodu odpovídá jeden řádek - pod které dej transformované body (stále List 4, 5 a 6) a spusť program HELMERT3 nebo HELMERT5
- přibližné transformační koeficienty se u programu HELMERT3 počítají pomocí prvních čtyř identických bodů
- v případě programu HELMERT3 se zobrazí nabídka s možností nové transformace nebo dalšího vyrovnání transformačních koeficientů (je lepší provést alespoň jedno další vyrovnání, dvojí výpočet oprav se jinak může lišit i o několik metrů)
- na displeji se budou zobrazovat informace o jednotlivých krocích transformace
- na konci výpočtu se zobrazí transformační koeficienty (TX, TY, TZ, q, α, β a γ), jejich střední chyby, aposteriorní střední chyba jednotková m0, střední souřadnicové chyby mX, mY, mZ, mXYZ a míra ztotožnění mV
- pokud se první a druhý výpočet oprav nebudou dostatečně shodovat (jejich rozdíly jsou uloženy v Listu 11 až 13), můžeš provést další vyrovnání transformačních koeficientů novým spuštěním programu HELMERT3
- výsledné hodnoty je možné dále dotransformovat pomocí Jungovy dotransformace

Zápis do Listů:
List 1: X - identické body v hlavní soustavě
List 2: Y
List 3: Z
List 4: x - identické body ve vedlejší soustavě + podrobné body které se budou transformovat
List 5: y
List 6: z
List 7: XT - výsledné souřadnice transformovaných bodů
List 8: YT
List 9: ZT
List 10: nic
List 11: rozdíl prvního a druhého výpočtu oprav pro X (v2-v1)
List 12: rozdíl prvního a druhého výpočtu oprav pro Y
List 13: rozdíl prvního a druhého výpočtu oprav pro Z
List 14: nic
List 15: druhý výpočet oprav pro X
List 16: první výpočet oprav pro X (v1=(ATA)-1ATl)
List 17: druhý výpočet oprav pro Y
List 18: první výpočet oprav pro Y
List 19: druhý výpočet oprav pro Z
List 20: první výpočet oprav pro Z

Hansenova úloha (748 B) - výpočet úhlů φ, ψ, μ a ν (obrázek, 2.11 kB) pro převod Hansenovy úlohy na protínání vpřed z úhlů (viz úloha 4 z GD20). ω1 až ω4 jsou úhly změřené na určovaných bodech

Polární stanovisko (1.99 kB)
Výpočet pravoúhlých souřadnic ze zadaných směrů a délek
POLARKA (450 B) - klasická polární metoda - údaje se zadávají po jeho spuštění (zapisují se do Listů)
POLARKA2 (216 B) - počítá s údaji uloženými v Listech 1 až 4
POLARKA3 (117 B) - polární metoda při měřených směrnících a délkách
Zápis do Listů:
List 1: souřadnice Y (stanovisko, orientace, určované body)
List 2: souřadnice X (jako u Y)
List 3: směry na orientaci a podrobné body
List 4: délky na podrobné body (u orientace dej 0)

Výpočet výměr (1.95 kB)
VYMERY (332 B) - výpočet výměr ze souřadnic zadaných po spuštění programu
VYMERY2 (185 B) - výpočet výměr ze souřadnic uložených v Listu 1 a 2
VYMERY3 (280 B) - výpočet výměr z polárních prvků zjištěných při zaměření pozemku na jednom stanovisku
- seznam zadaných bodů musí začínat i končit stejným bodem
Zápis do Listů:
List 1: Y
List 2: X
List 3: směry (u VYMERY3)
List 4: vzdálenost (u VYMERY3)

Výpočet vytyčovacích prvků (4.64 kB)
VYT_POL (371 B) - výpočet polárních vytyčovacích prvků ze souřadnic
Zápis do Listů:
List 1: Y
List 2: X
List 3: směr
List 4: vzdálenost
VYT_ORT (405 B) - výpočet ortogonální vytyčovacích prvků ze souřadnic
Zápis do Listů:
List 1: Y
List 2: X
List 3: směry (u VYMERY3)
List 4: vzdálenost (u VYMERY3)
VYTYC (902 B) 9x50 - výpočet polárních a ortogonální vytyčovacích prvků ze souřadnic zadaných po spuštění programu
VYTYC2 (624 B) 9x50 - výpočet ze souřadnic v Listu 1 a 2 (na řádku 1 je stanovisko, na 2 orientace)
Zápis do Listů:
List 1: Y
List 2: X
List 3: směr
List 4: vzdálenost
List 5: směr z orientace
List 6: vzdálenost z orientace
List 5: směrník stanovisko - vytyčovaný bod
List 8: staničení
List 9: kolmice (vpravo +, vlevo -)
List 10: doměrek ("staničení" od koncového bodu)

Vytyčení kružnicového oblouku (4.93 KB)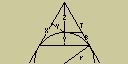
OBLK_HlB (202 B) - vytyčovací prvky hlavních bodů oblouku
OBLK_OB (245 B) - obrázek k vypočtu hlavních bodů oblouku
OBLK_PRE (434 B) - výpočet údajů pro vytyčení oblouku s přenášením stroje (úhel δ a vzdálenost r pro podrobné body a doplňkový úhel θ a doplňková vzdálenost pro koncový bod oblouku)
OBLK_PkS (489 B) - vytyčovací prvky pro konstantní úsek na oblouku
OBLK_PkT (419 B) - vytyčovací prvky pro konstantní úsek na tečně
OBLK_RED (129 B) - výpočet zkrácení (redukce) délky (oblouk na tětivu a tětiva na oblouk)
OBLK_Klo (541 B) - oblouk s klotoidou
Zápis do Listů (pro vytyčovací prvky podrobných bodů, jinak se údaje ukládají po pamětí):
List 1: staničení
List 2: kolmice
List 3: směr (kolmice vpravo, nula na průsečíku tečen)
List 4: vzdálenost
List 5: směr (komice vlevo)

Protínání (5.45 kB)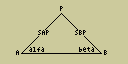
PRO_UHEL (212 B) a PRO_U (244 B) - protínání vpřed z úhlů
PRO_SMER (219 B) a PRO_S (255 B) - protínání vpřed z orientovaných směrů
PRO_DELK (252 B) a PRO_D (307 B) - protínání vpřed z délek
PRO_V_OB (189 B) - obrázek pro správné vložení údajů u protínání vpřed
PRO_ZPET (261 B) a PRO_Z (343 B) - protínání zpět
PRO_Z_OB (171 B) - obrázek k protínání vpřed
- programy jsou tam dvakrát, např. PRO_UHEL a PRO_U. První zobrazí pouze výsledek, druhý všechny kroky pro zápis do příslušného zápisníku

Hromadné protínání zpět (2.19 kB) 9x50*
PRO_ZP_n (400 B) - výpočet protínání zpět z více kombinací - zadej hodnoty do Listu 1 až 3 a spusť program
Pokud se odstraní zápis hodnot úhlů α a β do do Listu 8 a 9, je možné program použít i na kalkulačkách série 9x50
Zápis do Listů:
List 1: Y-ová souřadnice cíle
List 2: X-ová souřadnice cíle
List 3: směr na cíl
List 4: kombinace cílů
List 5: vypočítaná Y-ová souřadnice stanoviska v dané kombinaci
List 6: vypočítaná X-ová souřadnice stanoviska v dané kombinaci
List 7: nic
List 8: úhel α
List 9: úhel β

Polygonové pořady (9.60 kB) 9x50 (mimo volného PLG)
Jde o tyto polygonové pořady:
PLG_2P2O (1259 B) - oboustranně směrově a polohově připojený
PLG_2P1O (992 B) - vetknutý jednostranně orientovaný - souřadnicové vyrovnání je řešeno transformací
PLG_VET (948 B) - vetknutý polygonový pořad - souřadnicové vyrovnání je řešeno transformací
PLG_VOL (763 B) - volný polygonový pořad
PLG_UZAV (830 B) - polygonový pořad uzavřený
PLG_ORI (252 B) - pokud znáš na připojovacích bodech pouze směrníky na orientace (u PLG_2P2O a PLG_2P1O), můžeš dopočítat fiktivní souřadnice orientací (ve vzdálenosti 1000 m). Spusť PLG_2P2O nebo PLG_2P1O, zadej jako souřadnice orientace libovolná čísla a dále postupuj podle pokynů programu. Po skončení programu spusť PLG_ORI, zadej směrníky (u PLG_2P1O dej jako druhý nulu) a znovu spusť PLG_2P2O nebo PLG_2P1O s praveným počátkem zdrojového kódu (viz. pár řádků níž)
- výsledky se zapisují do Listu 1 a 2 . Po zadání jde opravit vstupní údaje (úhly, délky a souřadnice známých bodů) v Listech 1 až 4. Po změně začátku zdrojového kódu programu z `GoTo X na Goto X se při novém spuštění programu pořad přepočítá
Zápis do Listů:
List 1: souřadnice Y (počáteční ORI, počáteční připojení, určované body, koncové připojení, koncová ORI)
List 2: souřadnice X (jako u Y)
List 3: měřený úhel (na bodě kterému patří souřadnice)
List 4: délka vpřed (na bodě kterému patří souřadnice)
List 5: směrník
List 6: prozatímní souřadnicový rozdíl Y
List 7: prozatímní souřadnicový rozdíl X
List 8: opravený (přetransformovaný) souřadnicový rozdíl Y (nebo oprava)
List 9: opravený (přetransformovaný) souřadnicový rozdíl X (nebo oprava)
List 10: nic
List 11: transformace: λ1, λ2 (transformační koeficienty), M (zkreslení), φ (úhel otočení),
             SPK, SPK´(vzdálenost PK), OP (polohová odchylka), ΔP (mezní odchylka pro hlavní a vedlejší PLG)
List 12: úhlové vyrovnání: σP-Ori + Σω, 2R(n-1), σK-Ori , Oω (úhlová odchylka), Δω (mezní odchylka)
List 13: souřadnicové vyrovnání (Y): ΔyKP, ΣΔy, Σ|Δy|, Oy, OP, ΔP (pro hlavní a vedlejší PLG)
List 14: souřadnicové vyrovnání (X): ΔxKP, ΣΔx, Σ|Δx|, Ox

Vyrovnání oboustraně připojeného a orientovaného polygonového pořadu pomocí MNČ (6.15 kB) 9x50
PLG_VYR (2'917 B) - po spuštění programu zadej požadované hodnoty nebo je načti z Listu 1 až 4
Program počítá apriorní střední chyby a kovarianční matice (pokud chceš výpočet aposteriorních hodnot, musíš na začátku programu přiřadit do proměnné Q hodnotu 1)
Z kovarianční matice vyrovnaných souřadnic získáš střední chyby a parametry elips chyb pomocí programu MAT-KOV (pracuje s maticí Z)
Zápis do Listů:
List 1: souřadnice Y (počáteční ORI, počáteční připojení, vyrovnané body, koncové připojení, koncová ORI)
List 2: souřadnice X (jako u Y)
List 3: měřený úhel (na bodě kterému patří souřadnice)
List 4: délka vpřed (na bodě kterému patří souřadnice)
List 5: nic
List 6: vyrovnaný úhel
List 7: chyba vyrovnaného úhlu (v cc nebo '')
List 8: vyrovnaná dálka
List 9: chyba vyrovnané délky (v mm)

Zápis do Matic:
Matice D: derivace uzávěrů (x,y,ω) podle měřených délek a úhlů
Matice F: derivace vyrovnaných souřadnic podle vyrovnaných délek a úhlů
Matice M: kovarianční matice vyrovnaných délek a úhlů
Matice N: matice normálních rovnic (DP-1DT)-1
Matice P: matice vah měřených délek a úhlů
Matice K: matice korelát
Matice U: vektor uzávěrů (x,y,ω)
Matice V: vektor oprav měřených délek a úhlů
Matice X: kovarianční matice vyrovnaných souřadnic
Matice Y: kovarianční matice mezních uzávěrů

Operace s maticemi (1.41 kB)
MAT-DIA2 (89 B) - převede List 1 na diagonálu matice Z
MAT-DIAG (88 B) - převede diagonálu matice Z do Listu 1
MAT-KOV (384 B) - projde matici Z a ze submatic 2×2 na hlavní diagonále vypočítá střední chyby (mx, my, mp a mxy) a parametry elipsy chyb (a, b a ω)

Výpočet prvků matice A (1.48 kB)
DA_DELKA (116 B) - derivace délky
DA_SMER (143 B) - derivace směru
DA_UHEL (255 B) - derivace úhlu

Vyrovnání vázané sítě (1.17 kB)
SIT_VAZ (738 B) - výpočet vyrovnání vázané sítě pomocí vyrovnání měření zprostředkujících
Je třeba sestavit matice A a P a vektor l'
Pro práci s výslednými kovariančními maticemi použij programy MAT-DIAG a MAT-KOV
Zápis do Matic:
Matice A: derivace zprostředkujících podle neznámých
Matice P: matice vah zprostředkujících
Matice L: vektor redukovaných měření
Matice Q: matice normálních rovnic (ATPA)-1
Matice X: přírůstky neznámých
Matice V: opravy měřených hodnot
Matice M: kovarianční matice neznámých
Matice N: kovarianční matice zprostředkujících

Řešení sférického trojuhelníku na kouli (2.72 kB)
SFERA_K (1506 B) - výpočet případu SSS, UUU, SUS, USU, SSU a SUU
- poloměr koule je možno změnit na řádku 4
- není ošetřen výpočet úhlů pomocí sinové věty (pro úhly větší než 90°. Pokud to nevychází správně, je vypočtený úhel doplněk do 180°)

Průsečík ortodrom (1.39 kB)
PRUS_ORT (777 B) - určení průsečíku dvou ortodrom
- každá ortodroma se zadá pomocí dvojice bodů

Výpočet základních geodetických úloh na kouli (1.33 kB)
GU_Koule (684 B)
1. GU = z bodu zadaného šířkou, délkou a azimutem vypočti bod (jeho šířku, délku a azimut) v určité vzdálenosti
2. GU = ze dvou zadaných bodů vypočti jejich vzdálenost a azimuty ortodromy v těchto bodech
- výpočet se provádí na kouli o poloměru R=6380 km (možno změnit na řádku 5)

Jungova dotransformace (1.45 kB) 9x50
- obvykle se používá pro ztotožnění identických bodů po Helmertově transformaci
JUNG-2D (260 B)
- do Listu 1 a 2 zadej původní souřadnice identických bodů, do Listu 3 a 4 jejich přetransformované souřadnice a pod ně souřadnice podrobných bodů (každému bodu odpovídá jeden řádek). Poté spusť program JUNG-2D. Výsledky se zapíší do Listu 5 a 6
- nezáleží na pořadí souřadnic (X/Y nebo Y/X), jen je třeba je zachovat u všech bodů
Zápis do Listů:
List 1: původní X-ové souřadnice identických bodů
List 2: původní Y-ové souřadnice identických bodů
List 3: přetransformované X-ové souřadnice identických bodů a souřadnice podrobných bodů
List 4: přetransformované Y-ové souřadnice identických bodů a souřadnice podrobných bodů
List 5: X-ové souřadnice bodů po Jungově dotransformaci
List 6: Y-ové souřadnice bodů po Jungově dotransformaci

JUNG-3D (360 B)
- do Listu 1 až 3 zadej původní souřadnice identických bodů, do Listu 4 až 6 jejich přetransformované souřadnice a pod ně souřadnice podrobných bodů (každému bodu odpovídá jeden řádek). Poté spusť program JUNG-3D. Výsledky se zapíší do Listu 7 až 9
- nezáleží na pořadí souřadnic (X/Y nebo Y/X), jen je třeba je zachovat u všech bodů
Zápis do Listů:
List 1: původní X-ové souřadnice identických bodů
List 2: původní Y-ové souřadnice identických bodů
List 3: původní Z-ové souřadnice identických bodů
List 4: přetransformované X-ové souřadnice identických bodů a souřadnice podrobných bodů
List 5: přetransformované Y-ové souřadnice identických bodů a souřadnice podrobných bodů
List 6: přetransformované Z-ové souřadnice identických bodů a souřadnice podrobných bodů
List 7: X-ové souřadnice bodů po Jungově dotransformaci
List 8: Y-ové souřadnice bodů po Jungově dotransformaci
List 9: Z-ové souřadnice bodů po Jungově dotransformaci

Výpočet azimutu (1.4 kB)
AZIMUT (800 B) - po zadání souřadnic y a x v S-JTSK dvou bodů spočte azimut takto dané spojnice včetně směrové korekce δ

Výpočet směrových korekcí δ12 a δ21 (1.78 kB)
KOREKCE (620 B) - po zadání souřadnic koncového a počátečního bodu spojnice spočte směrové korekce δ12 a δ21 . Výsledek je v šedesátinných ('') a setinných (cc) vteřinách

Výpočet matic A, D, P a l' pro vyrovnání pomocí vyrovnání měření zprostředkujících (18.90 KB)
Mat_ADPl (947 B) - před vlastním výpočtem je třeba vytvořit seznam souřadnic všech bodů které budou pro výpočet použity (známé body a přibližné souřadnice bodů určovaných (vyrovnávaných)) a zadat pořadí určovaných (vyrovnávaných) bodů. Viz
Zápis do Listů:
List 1: číslo bodu
List 2: Y-ová souřadnice bodu
List 3: X-ové souřadnice bodu
List 6: pořadí čísel vyrovnávaných bodů

Pro výpočet se používá několik podprogramů:
podprogramy:
PP-BOD (222 B) - vyhledání bodu v seznamu souřadnic
PP-DELKA (324 B) - výpočet prvků matic pokud je jako zprostředkující délka
PP-SMER (512) - výpočet prvků matic pokud je jako zprostředkující směr
PP-UHEL (700) - výpočet prvků matic pokud je jako zprostředkující úhel

Během výpočtu se vytváří několik matic:
Zápis do Matic:
Matice A: derivace zprostředkujících podle neznámých. Pokud je jako zprostředkující použit úhel nebo směr, je hodnota vynásobena konstantou ρ podle aktivní úhlové míry
Matice D:  derivace měření podle neznámých (pro výpočet matice P = (DT*PD)-1)
Matice *P: matice vah měření. Pokud je jako zprostředkující vzatý směr na určovaném bodě, je třeba příslušný řádek správně upravit (1 prvek dube mít hodnotu 1 a t prvků hodnotu 1/t (t je počet orientací na známé body))
Matice L: vektor měření spočtených ze souřadnic. Hodnoty jsou v metrech nebo grádech či stupních
Matice T: slouží pro převod vektoru l (Matice L) z metrů a grádů (stupňů) na milimetry a vteřiny (Mat T×Mat L(m/g/°))
Matice U: slouží pro převod převedeného vektoru l (Matice L) z milimetrů a vteřin na metry a grády (stupě) (Mat U×Mat L(mm/cc/''))




Sestavení matic lze kdykoliv opustit a pokračovat v něm později, rovněž je možné vynulování špatně zadaných řádků

Výpočet plochy na elipsoidu (0.96 KB)
PLCH_ELI (392 B) - po zadání zeměpisné šířky φ a délky λ krajních poledníků a rovnoběžek vypočte plochu daného lochoběžníku
- výpočet probíhá na Besselově elipsoidu (úpravou parametrů A a E lze nadefinovat libovolný elipsoid)

Parametry elipsoidů (1.34 KB)
ELI (1026 B) - přehled parametrů různých elipsoidů (Besselův, Krasovského, Hayfordův, GRS-80 (Geodetic Reference System 1980) a WGS-84 (World Geodetic System 1984))

Kartografie

JTSK↔φλ (3.18 kB)
JTSK2FL (966 B) - převod pravoúhlých souřadnic Y, X v S-JTSK na polární ρ a ε, kartografickou šířku a délku Š a D, zeměpisnou šířku a délku na referenční kouli U a V a zeměpisnou šířku a délku na Besselově elipsoidu φ a λ (od Ferra a od Greenwiche) a určení Křovákova koeficientu m a meridiánové konvergence C
- výsledky se vypisují ve tvaru:

126°25'36.5''
36.4856987

kde to spodní číslo znamená vteřiny na maximální počet desetinných míst (kalkulačka normálně zobrazí nejvýše dvě, což v některých případech nemusí stačit)

FL2JTSK (945 B) - převod zeměpisných souřadnic φ a λ na rovinné Y a X v S-JTSK s mezivýsledky (viz. program JTSK2FL)

Výpočet loxodromy (987 B)
LOXODROM (528 B) - určení azimutu, délky a dopočet délky a šířky pro zadanou šířku nebo délku
- výpočet se provádí na kouli o poloměru R=6380 km (možno změnit na řádku 4)

Výpočet ortodromy (2.19 kB)
ORTODROM (1329 B) - ortodromu je možné zadat pomocí bodu a azimutu nebo pomocí dvou bodů
- program poté vypočte šířku nejsevernějšího bodu a nabídne dopočet šířky a délky pro zadanou šířku nebo délku (asi půlka programu se zabývá řešením kvadrantů)
- výpočet se provádí na kouli o poloměru R=6380 km (možno změnit na řádku 5)

Astronomie

Transformace mezi systémy (5.80 KB)
aSe_Sr2 (443 B) a aSr2_Se (394 B) - převod mezi ekliptikální (Se) a druhou rovníkovou soustavou (Sr2)
aSr2_Sr1 (370 B) a aSr1_Sr2 (374 B) - převod mezi první (Sr1) a druhou (Sr2) rovníkovou soustavou
aSr1_So (402 B) a aSo_Sr1 (408 B) - převod mezi obzorníkovou (So) a první rovníkovou (Sr1) soustavou
aXYZ-S_ (642 B) - převod pravoúhlých souřadnic na sférické (ekliptikální, obzorníkové a první a druhá rovníková soustava)

Východ a západ (1.07 KB)
aVychZap (576 B) - určení času východu a západu ze známé deklinace δ a rektascenze α hvězdy a zeměpisné šířky φ stanoviska

Průchod horní a dolní kulminací (639 B)
aKulmin (358 B) - určení času horní a dolní kulminace známé deklinace δ hvězdy a zeměpisné šířky φ stanoviska

Průchod prvním vertikálem nebo elongací (1.68 KB)
aVer_Elo (977 B) - určení času průchodu prvním vertikálem nebo elongací ze známé deklinace δ a rektascenze α hvězdy a zeměpisné šířky φ stanoviska

Teorie chyb

TC (6.96 KB)
TC-FI.t (99 B) - výpočet hustoty pravděpodobnosti φ(t)
TC-G.t (93 B) - výpočet hodnoty Laplaceovy funkce G(t) - oboje se jinak interpoluje v tabulkách
TC-Binom (182 B) - výpočet členů binomického rozvoje
TC-NR (631 B) - výpočet pravděpodobnosti a parametrů pořadnice y Gaussovy a sumační křivky na zadaném intervalu

Výpočet průměru (0.93 KB) - výpočet průměru, m0 a m hodnoty
TC-P.ARI (171 B) - aritmetický průměr
TC-P.VAZ (232 B) - vážený průměr
Zápis do Listů:
List 1: hodnoty ze kterých se počítá průměr
List 2: případné příslušné váhy

Dvojice měření (1.45 KB) - výpočet vyrovnané hodnoty a středních chyb (md, m0, mx a mF)
TC-DV.BV (439 B) - dvojice měření s vahami
TC-DV.SV (455 B) - dvojice měření bez vah
List 1: měření TAM
List 2: měření ZPĚT
List 3: případné příslušné váhy

TC10 (2.25 kB) - výpočet prvních tří úloh z TC10
TC10-1 (406 B) - vývoj statistické pravděpodobnosti
do Listu 2 zadej počet příznivých případů v dvojici a spusť program. Výsledky v Listu 1 až 4 odpovídají požadované tabulce, je možné i zobrazení grafu
TC10-2 (406 B) - binomické rozdělení pravděpodobnosti
po spuštění programu zadej počet hodů a poměr (čitatel:jmenovatel). Vypočte se střední hodnota a hodnoty pro graf
Zápis do Listů:
List 1: k - pořadí v binomickém rozvoji
List 2: p* - graf
List 3: σ100 - očekávaná odchylka pro n = 100
List 4: σ1000 - očekávaná odchylka pro n = 1000
TC10-3.1 (406 B) 9x50 - srovnání normálního rozdělení se skutečností
do Listu 2 zadej hodnoty z histogramu (sloupcový graf), na pátém řádku programu případně uprav meze (nastaveno je -3.6 až 3.6) a spusť program. Zadej střední uzávěr m a čekej (výpočet trvá asi 20 vteřin). Výsledky se zapisují do Listu 1 až 15 přičemž jeden List odpovídá jednomu řádku tabulky
TC10-3.2 (186 B) - porovnání skutečného a teoretického procenta uzávěrů ležících v t-násobku střední kvadratické chyby
do Listu 3 zadej absolutní četnost, spusť program a zadej m. Jednotlivé řádky odpovídají požadované tabulce

Optika

programy jsou dělané pro laborky z optiky

Úloha 7.1 (977 B)
U prvního směru (9°) zadej do Listu 2 minuty a do Listu 3 vteřiny. Susť program a zadej úhel (9°)*. Zobrazí se ti průměrná velikost směru kolmice a střední chyba kolmice. Poté zadej číslo počítané kolmice** (1 = směr 9°, 2 = směr 99° a 3 = směr 234°)
U druhého a třetího směru nahraď měřené minuty a vteřiny v listech 2 a 3 příslušnými daty (ostatních listů si zatím nevšímej) a znovu spusť program (jako úhel tentokrát zadej 99° a 234°). Po zadání čísla směru tři se vypočtou lámavé úhly, jejich součet a chyby. Chyby měřených hodnot jsou uloženy v listu 7 pro první směr, v listu 8 pro druhý směr a v listu 9 pro třetí směr
* směry budou pravděpodobně 9°, 99° a 234°
** program je dělaný tak, že se směry musí počítat v pořadí 9° - 99° - 234°

Úloha 7.2 (843 B)
Určení tloušťky čočky - do listu 1 zadej ai, do listu 2 bi, spusť program a zvol určení tloušťky čočky. Zobrazí se ti tloušťka a střední chyba určení. V listu 3 pak najdeš rozdíl di a v listu 4 chyby di
Poloměr výbrusu sférických ploch - do listu 1 zadej ci a do listu 2 ei. Spusť program a zvol co chceš spočítat. Zobrazí se ti poloměr a jeho chyba. V listu 3 pak bude součin ci a ei

Úloha 7.3 (486 B)
Program je dělaný s předpokladem že se měří jen úseky stupnice 2, 4, 6 a 8 mm (10 a 12 se neměří kvůli velké vzdálenosti od středu čočky). Do listu 1 zadej aiP, do listu 2 aiL, do listu 3 biL a do listu 4 biP. Spusť program a vyleze ti ohnisková vzdálenost a její chyba. V list 5 pak najdeš rozdíl ai, v listu 6 rozdíl bi, v listu 7 ohniskovou vzdálenosti pro jednotlivé úseky a v listu 8 chybu této ohniskové vzdálenosti

Úloha 7.4 (352 B)
Program počítá hodnoty vždy pro jeden filtr. Do Listu 1 dej τ1, do Listu 2 τ2 a spusť program. Zobrazí se ti průměrná hodnoty a chyba. V Listu 3 je pak koeficient propustnosti pro každou dvojici (τi) a v Listu 4 jeho chyba (vi)

Různé

Kalendář (1.49 kB) (831 B) - jednoduchý kalendář (nejde o můj program)

GetKey (240 B) (42 B) - program který zobrazí kód naposledy stisknuté klávesy

Spořiče (4.23 kB) - několik prográmků vykreslujících různé obrazce

TOPlist